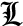 ANCELOT B
ANCELOT B-
is the latest release of LANCELOT,
and is designed to solve large-scale optimization problems
involving the minimization of a nonlinear objective, subject
(perhaps) to linear or nonlinear equality and box
constraints. All functions involved are assumed to be group
partially separable, and the minimization is based on a
Sequential Augmented Lagrangian algorithm. The new release
is coded in Fortran 95, allows for a non-monotone
descent strategy, Moré and Toraldo-type projections,
optional use of Lin and Moré's
ICFS
preconditioner, structured trust regions, and more.
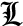 ANCELOT_SIMPLE
ANCELOT_SIMPLE-
is a simple-minded interface to LANCELOT
for small, dense problems.
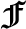 ILTRANE
ILTRANE-
is a package for finding a feasible point
for a set of linear and/or nonlinear equations and
inequalities using a multi-dimensional filter trust-region
approach. In the event that the system is inconsistent, a
local measure of infeasibility is minimized. Core linear
algebraic requirements are handled by an adaptive
preconditioned CG/Lanczos iteration.
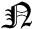 LS
LS-
is a package for minimizing an
objective function that is expressed as a sum of squares.
Advantage can be taken of second derivatives to produce
more accurate local models.
Both direct and iterative procedures are used to solve
core algebraic subproblems.
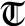 RU
RU-
solves the unconstrained optimization
problem using a trust-region method.
Both direct and iterative solution of core subproblems
is possible, and there are many other
"bells and whistles".
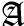 RC
RC-
solves the same
problem using an adaptive cubic regularization method.
Most of the features available with TRU are also
present here.
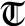 RB
RB-
solves the bound-constrained optimization
problem using a projected trust-region method.
Both direct and iterative solution of core subproblems
is possible, and again there are many other helpful
features".
 P
P-
provides a unified interface to all
the GALAHAD quadratic programs packages and enables
optional automatic problem scaling and pre/post-solution.
 PB
PB-
solves quadratic programs using a
primal-dual interior-point method globalized by means of a
trust region. The method works in two phases, the first
finding a feasible point for the set of constraints, while
the second maintaining feasibility while iterating towards
optimality. Once again, core linear algebraic requirements
are handled by an adaptive preconditioned CG/Lanczos
iteration.
 PA
PA-
is an active-set quadratic programming
solver which can also treat l_1 quadratic programs. At each
iteration, a step is computed along a direction which solves
an equality-constrained quadratic program whose constraints
are defined by a working subset of the currently active
constraints. Although, in general, QPB is to be preferred,
QPA is most useful when warm-starting a perturbation of a
previously-solved problem.
 PC
PC-
is a crossover quadratic programming
solver which applies successively QPB and QPA. The former is
used to obtain a good estimate of the solution at low cost,
while the latter refines the solution. Of particular note,
the optimal active set given by QPC is more reliable than
that from QPB.
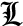 SQP
SQP-
uses a primal-dual interior-point method
to solve a linear or separable convex quadratic program.
Alternatively, it may also be used to compute the analytic
center of the feasible set, if it exists.
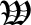 CP
CP-
uses a primal-dual interior-point method
to find a well-centered interior point for a region defined
by a finite number of linear equality and inequality
constraints. If the region is feasible but has no interior,
inequality constraints which must always be active are
identified.
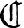 QP
QP-
solves convex quadratic programs using a
high-order primal-dual extrapolation method. The main
design feature is to allow fast convergence even when
the problem is degenerate using Puiseux rather than Taylor
expansions.
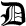 QP
QP-
solves strictly-convex quadratic programs
using a
dual gradient-projection method. The simplicity of the dual
feasible region allows for fast iterative solution.
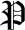 RESOLVE
RESOLVE-
is a quadratic program preprocessor. It
aims to apply inexpensive transformations to a given
quadratic program, so as to simplify it before passing it to
one of the other GALAHAD solvers. Once the solver has
completed its task, a post-processing stage may be used to
recover the original problem and its solution.
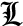 PB
PB-
solves linear programs using a
high-order primal-dual extrapolation methd, and is a
simplification of QPB.
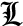 PA
PA-
solves linear programs using the
simplex method, but in reality is simply a convenient
wrapper to the HSL code LA04 that must be obtained
separately.
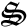 CALE
CALE-
provides a variety of quadratic program
scaling schemes that try to remove the effects of poor
problem scaling.
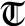 RS
RS-
solves the problem of minimizing a
quadratic subject to an ellipsoidal trust-region constraint,
by sparse-matrix factorizaion. The algorithm may also be
used to minimize the quadratic over the boundary of the
trust region, and allows additional linear equality
constraints
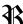 QS
QS-
solves the problem of minimizing a
quadratic subject plus a regularisation term penalising a
weighted two-norm of the variables, by sparse-matrix
factorization. Again, the algorithm permits additional linear
equality constraints
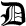 PS
PS-
finds a norm so that the minimizer of
the trust-region and regularized quadratic subproblems
require a single factorization, and solves the resulting
problems
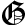 LTR
LTR-
solves the problem of minimizing a
quadratic subject to an ellipsoidal trust-region constraint,
using a Krylov method. The algorithm does not require any
factorization of the Hessian and may also be used to
minimize the quadratic over the boundary of the trust
region.
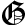 LRT
LRT-
solves the problem of minimizing a
quadratic subject plus a regularisation term penalising a
weighted two-norm of the variables, using a Krylov method.
Again, the algorithm does not require any factorization of
the Hessian.
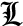 STR
STR-
solves the problem of minimizing the
two-norn of the deviation Ax-b subject to an ellipsoidal
trust-region constraint, using a Krylov method. The
algorithm does not require any factorization of A.
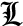 SRT
SRT-
solves the problem of minimizing the
square of the two-norn of the deviation Ax-b plus a
regularisation term penalising the two-norm of the
variables, using a Krylov method. Again, the algorithm does
not require any factorization of A.
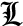 2RT
2RT-
solves the problem of minimizing the
two-norn of the deviation Ax-b plus a regularisation term
penalising the two-norm of the variables, using a Krylov
method. Once again, the algorithm does not require any
factorization of A.
 LLS
LLS-
solves the problem of minimizing the
two-norn of the deviation Ax-b subject to lower and
upper bounds on the variables, using a projected Krylov
method. The
algorithm does not require any factorization of A.
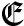 QP
QP-
solves quadratic programming problems for
which all the constraints are equations.
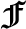 DC
DC-
determines whether a system of linear
equations is of full rank, and identifies a maximal subset
which may be removed without changing the rank
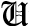 GO
GO-
find the global minimizer of
a smooth function of one variable over a specified finite
interval.
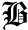 GO
GO-
find an approximation to the global
minimizer of a smooth function of several bounded variables
using a combination of stochastic, deterministic and
local optimization techniques.
 GO
GO-
find an approximation to the global
minimizer of a smooth function of several bounded variables
using an enhanced partition-and-bound method.
 BLS
BLS-
provides a variety of preconditioners
which may be applied when solving saddle point
(alternatively augmented, KKT) systems of linear
equations.
 SLS
SLS-
provides a variety of preconditioners
for sparse, unstructured symmetric matrices.
 LS
LS-
provides a generic interface
to a variety of external symmetric linear equation solvers
(HSL, SPRAL, PARDISO, WSMP), some of which are designed
for fast solution on shared-memory multiprocressing system.
Out-of-core solution is also supported.
 LS
LS-
provides a generic interface
to a variety of external unsymmetric linear equation solvers
from HSL. Future support for other solvers is planned.
![[Galahad Logo]](./galahad.small.gif)